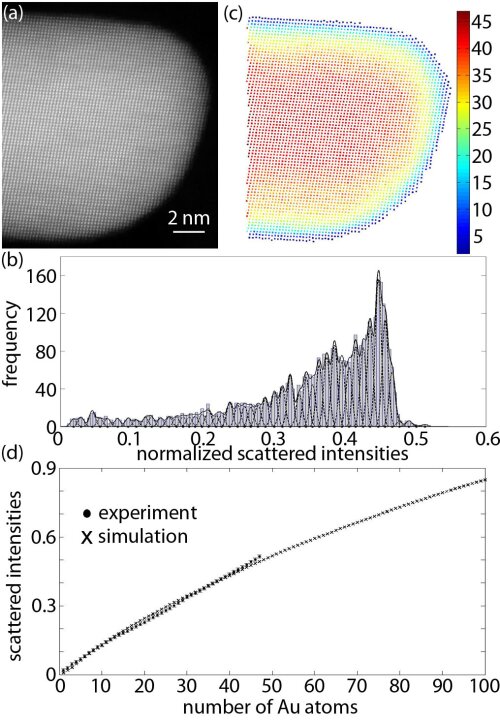
Measurements down to picometer precision
In recent years, visual interpretability of electron microscopy images was significantly improved by aberration corrected electron optics. Instrumental resolution limits down to 0.5 Å can nowadays be achieved. Still, in order to properly interpret all information contained in an atomic resolution image and to measure atomic displacements with picometer precision, quantitative methods are required. For this purpose, statistical parameter estimation is a powerful tool. The aim of statistical parameter estimation theory is to measure unknown structure parameters, such as atom positions and atom types, as accurately and precisely as possible from experimental electron microscopy images. Therefore a parametric model describing the expectations of the experimental measurements is used. This is a physics-based model depending on the unknown structure parameters. It describes the interaction of the electrons with the object, the transfer in the microscope, and the detection. Next, the unknown parameters are estimated by fitting this model to the experimental measurements using a criterion of goodness of fit which quantifies the similarity between the experimental measurements and the model.
Using statistical parameter estimation theory, atom column positions can be estimated with a precision of 1 pm when applied to reconstructed electron exit waves. This precision is sufficient to measure, for example, Ti displacements of only 3-6 pm inside a twin boundary in CaTiO3 (see figure). These displacements can be linked with the generation of ferroelectricity by interfaces inside this material.
Statistical parameter estimation theory also allows one to count the number of atoms in each atomic column when applied to HAADF STEM images. Using statistical parameter estimation theory, the total intensity of scattered electrons can be quantified atomic column - by - atomic column. This measure is sensitive to the number of atoms in an atomic column. To illustrate this, scattered intensities of all Au columns have been estimated from an aberration corrected HAADF STEM image of a Au nanorod (a). These intensities, shown in the form of a histogram (b), are expected to increase monotonically with the number of Au atoms present in a column. However, owing to a combination of experimental detection noise and residual instabilities, broadened - rather than discrete – peaks are observed. Therefore, these results cannot be interpreted directly in terms of number of atoms in a column. By evaluating the so-called integrated classification likelihood criterion, the presence of 47 significant peaks has been found. From the estimated peak positions, the number of Au atoms has been quantified (c). The experimental mean intensities (corresponding to the peak positions (b)) have been compared with the scattered intensities resulting from frozen phonon calculations under the same experimental conditions. The excellent match of the experimental and simulated intensities within the expected 5%–10% error range validates the accuracy of the obtained atom counts.
FIGURE LEGEND
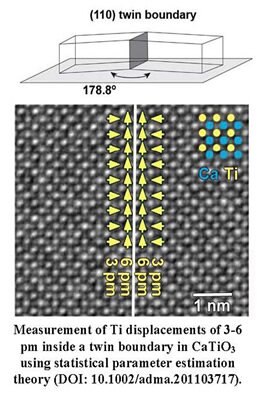
(a) HAADF STEM image of a Au nanorod. (b) Histogram of scattered intensities of the Au columns together with the estimated underlying distribution. (c) Number of Au atoms per column. (d) Comparison of experimental and simulated scattered intensities
(DOI: 10.1103/PhysRevB.87.064107).